差の二乗和の最小化と差の絶対値和の最小化

二乗和と絶対値和

前提条件

• $N$個からなる数列$A$が与えられる
• ある任意の実数$x$がある

差の二乗和は以下の式で示されます

$$S = \sum_{i=1}^{N}(A_i - x)^2$$

差の絶対値和は以下の式で示されます

$$S = \sum_{i=1}^{N}abs(A_i-x)$$

$abs$は絶対値のことです

二乗和を最小にするx

与式を見ると下に凸の２次関数です。つまり、関数の傾きが0の時総和は最小です。

式に落とし込みます

$$\frac{dS}{dx} = \sum_{i=1}^{N}(-2A_i + 2x) = 0$$

整理すると、

$$\sum_{i=1}^{N}A_i = Nx$$

変形すると、

$$\frac{1}{N}\sum_{i=1}^{N}A_i = x$$

ここで、$\frac{1}{N}\sum_{i=1}^{N}A_i$は数列$A$の平均値です。つまり、二乗和を最小にする$x$は平均値であることが証明されました。

絶対値和を最小にするx

数式で証明するのは難しいので図を用いて考えます。

$|A_i - x|$というのは数直線上の距離になります。

もし、$x$以下の値の数より、$x$以上の数が多い場合、$x$を増やすと総和が減ります。反対の場合も同様です。

図を見るとイメージしやすくなると思います。１幅１としてください。

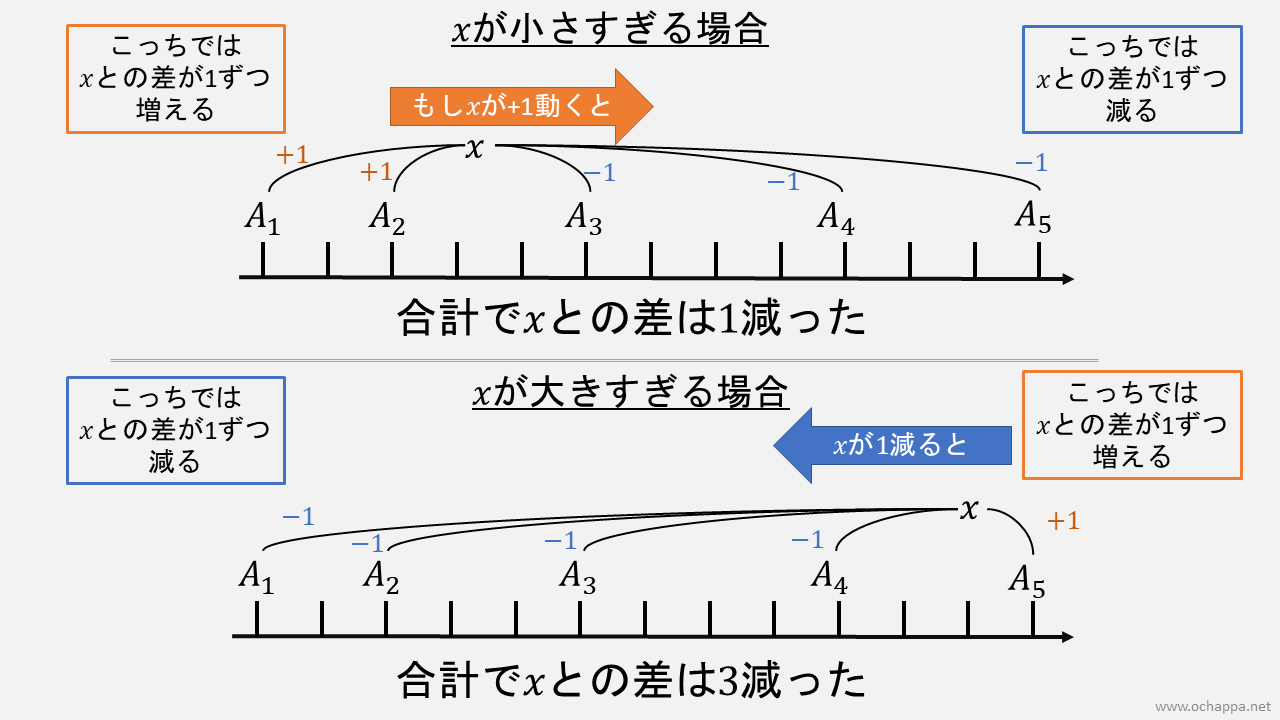
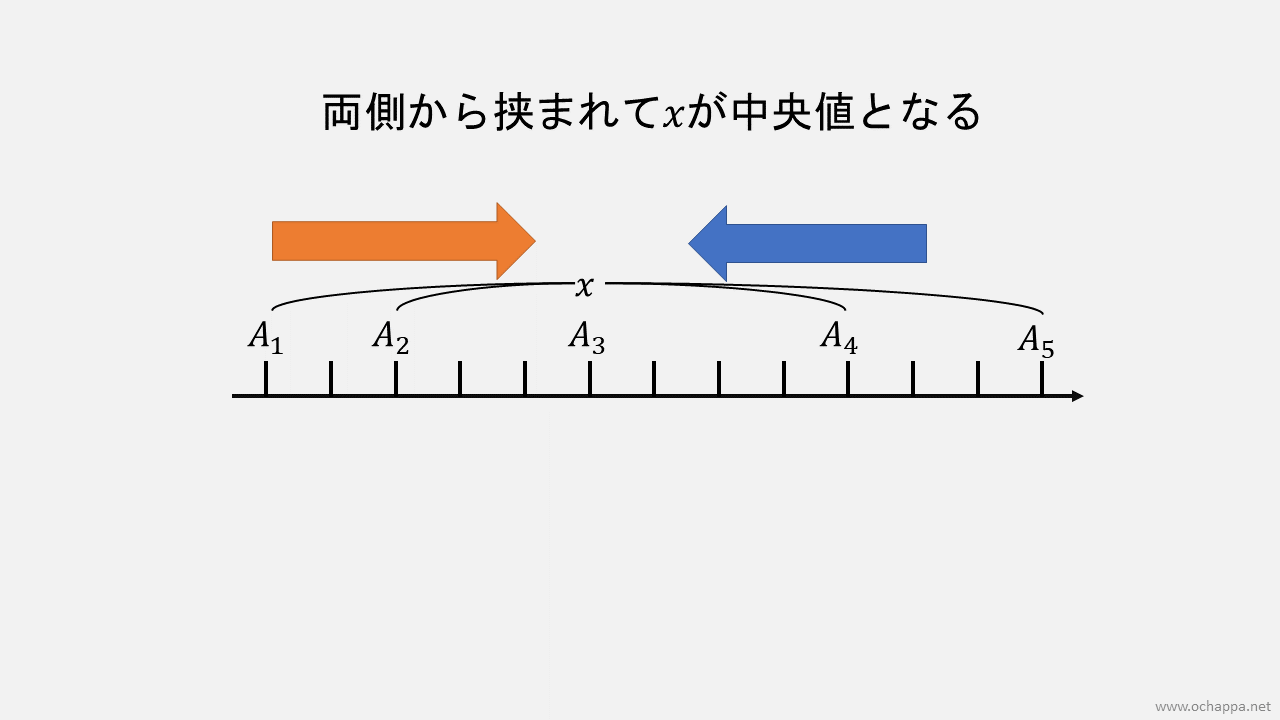
両側から攻めると、中央値になります。

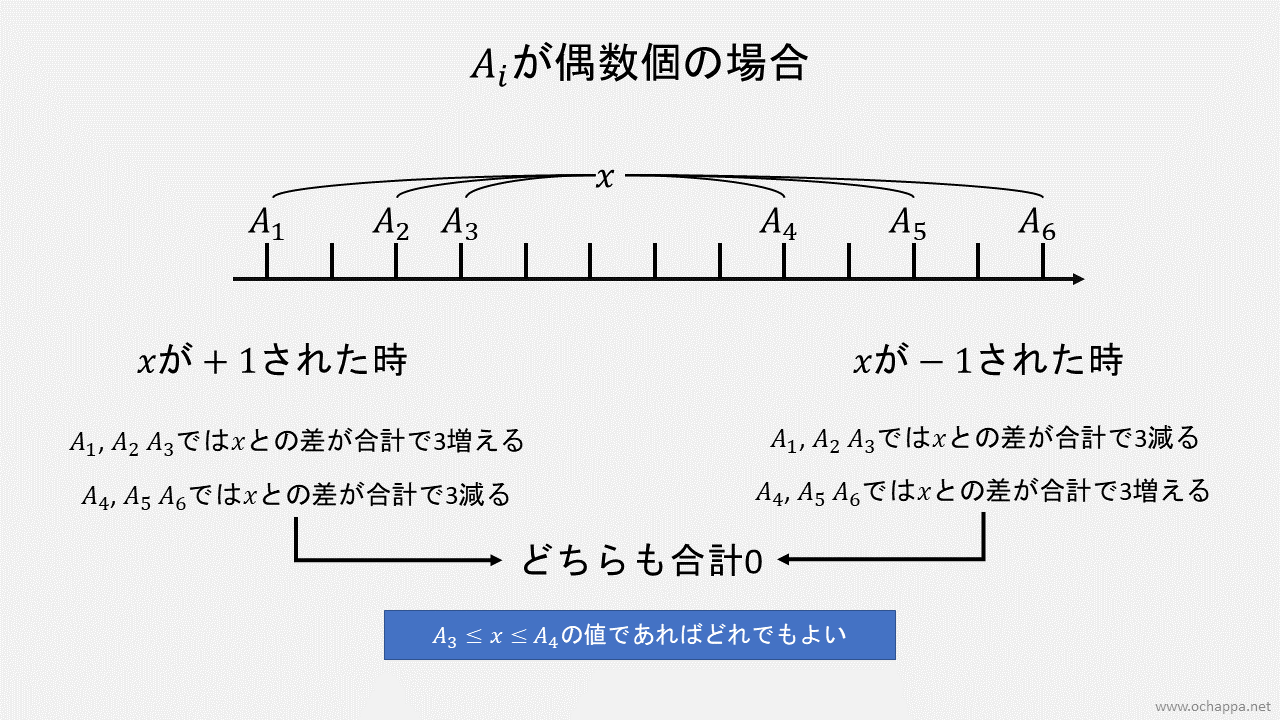
数列の長さが偶数個の場合は少し特殊です。