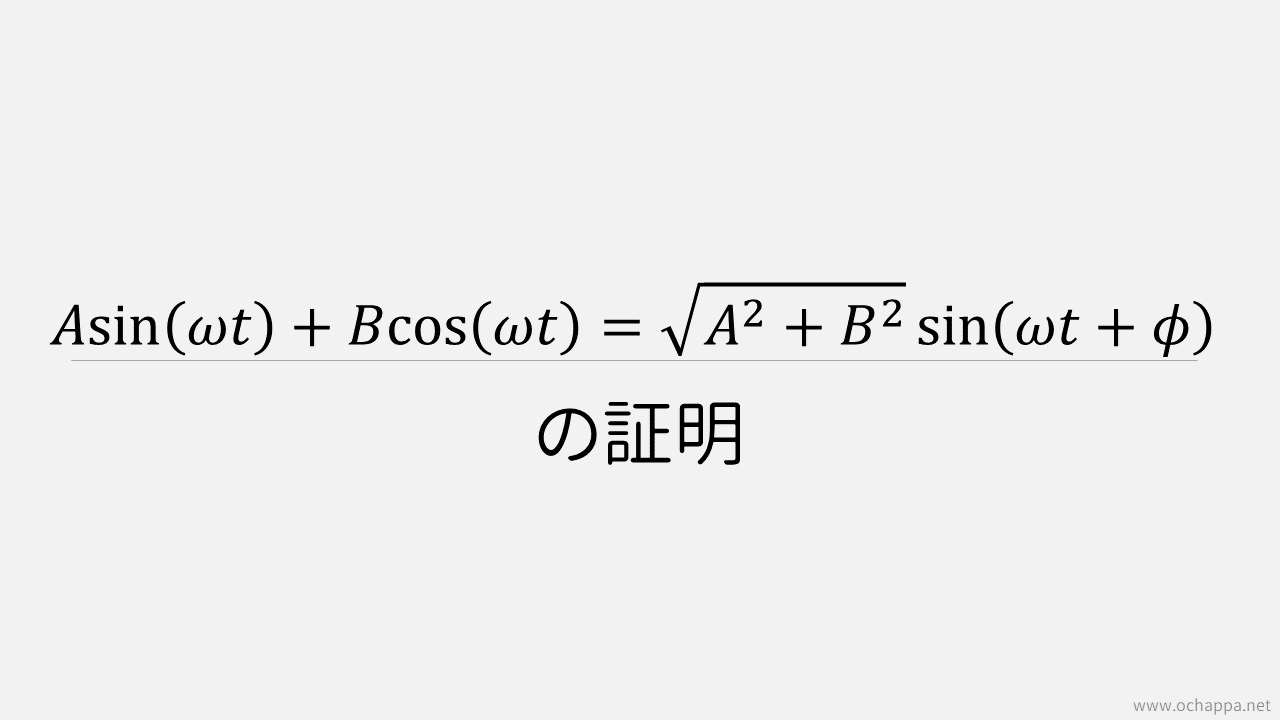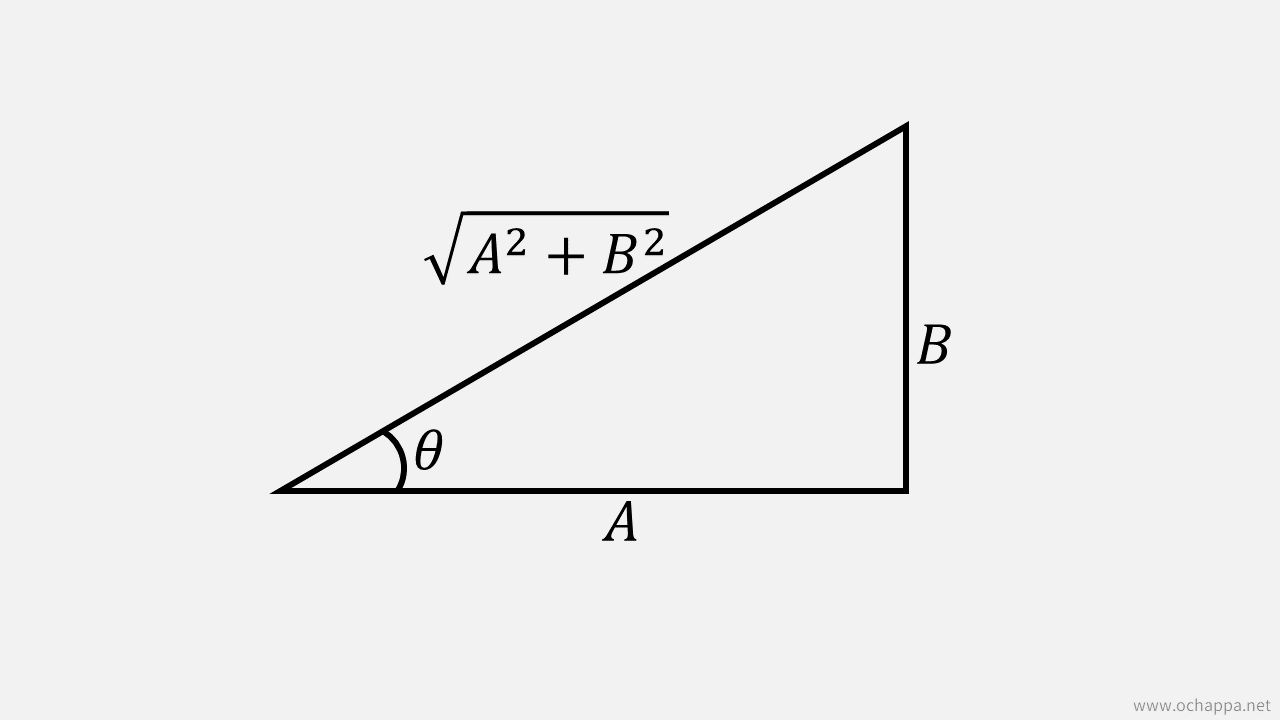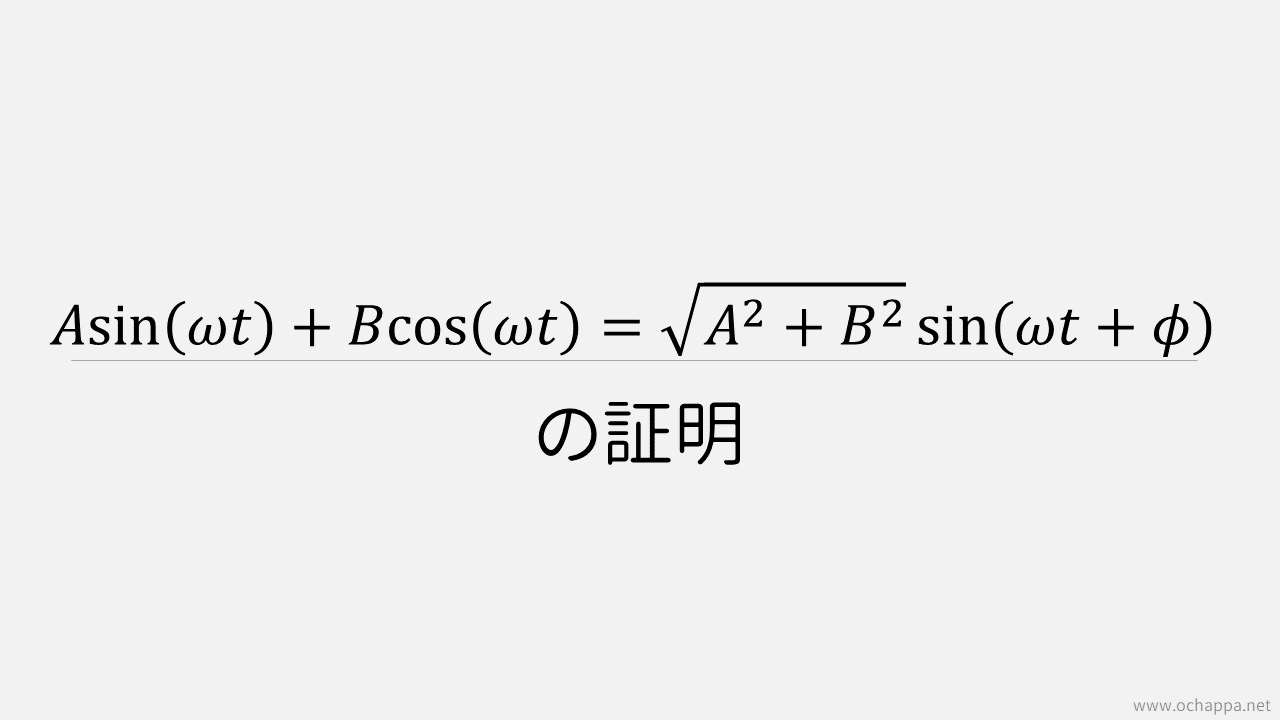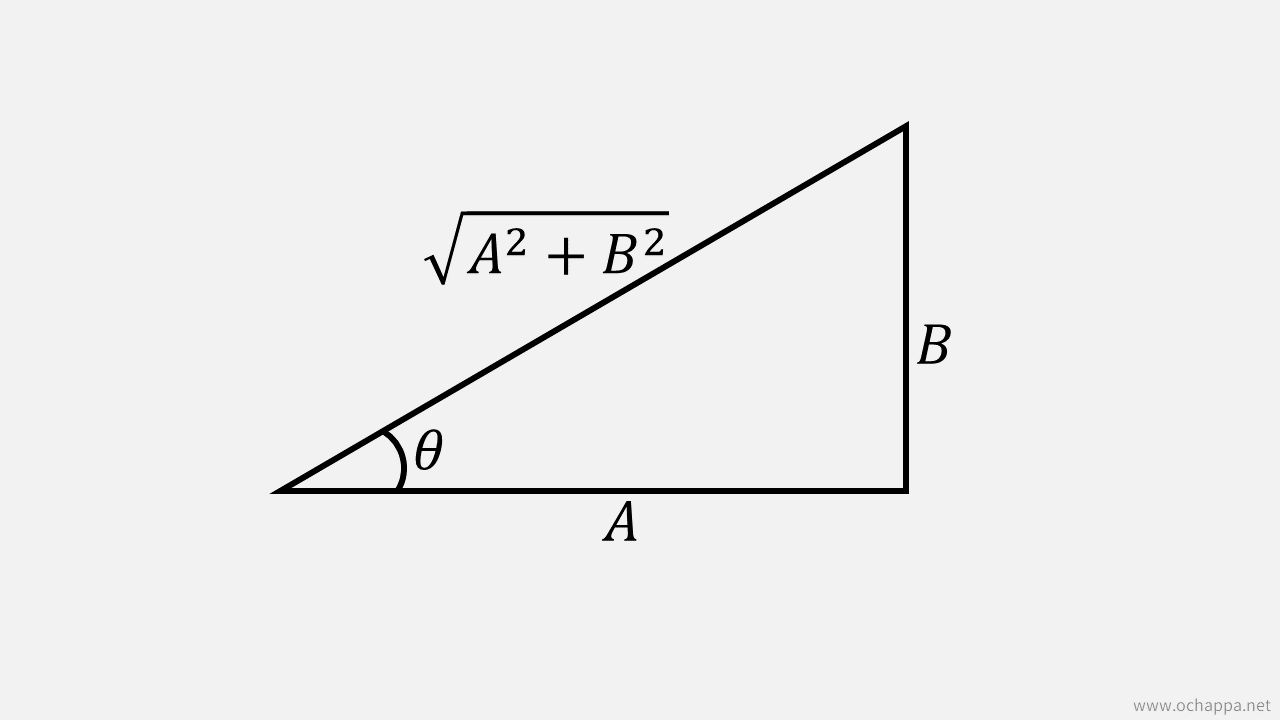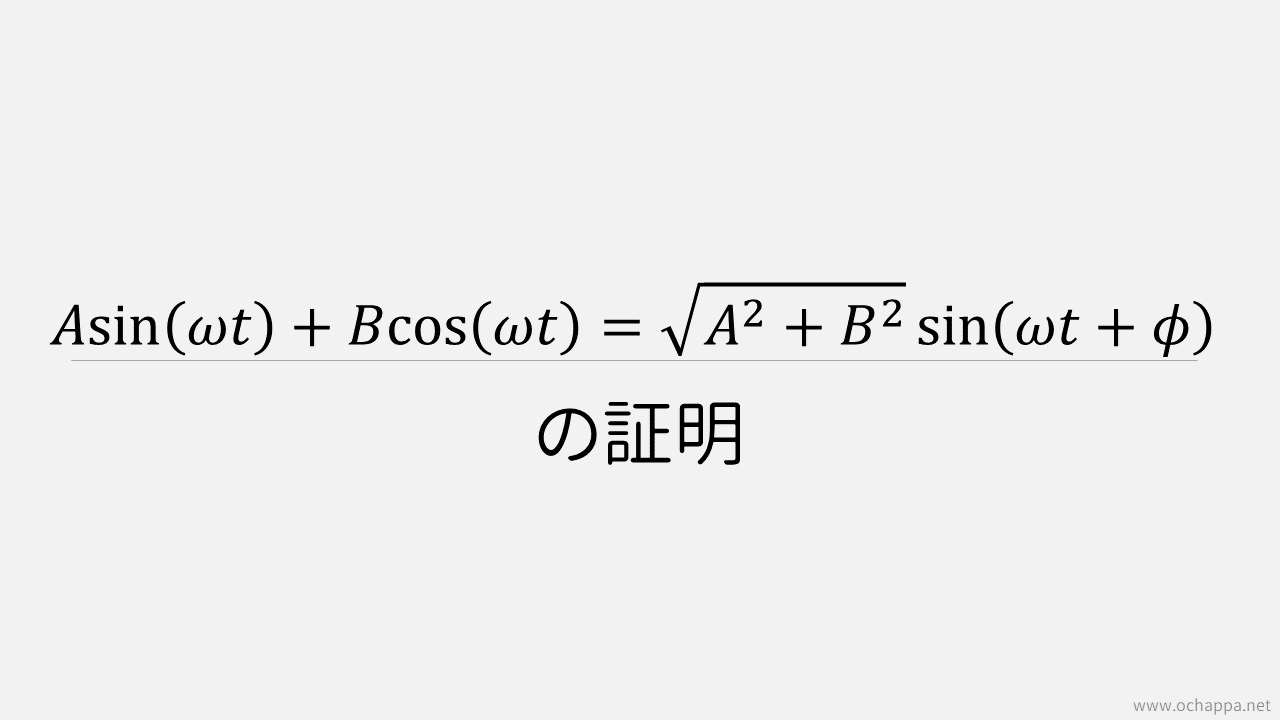
交流回路の計算でよく見かけます
証明
Asin(ωt)+Bcos(ωt)
まず、以下のような直角三角形を考えます。
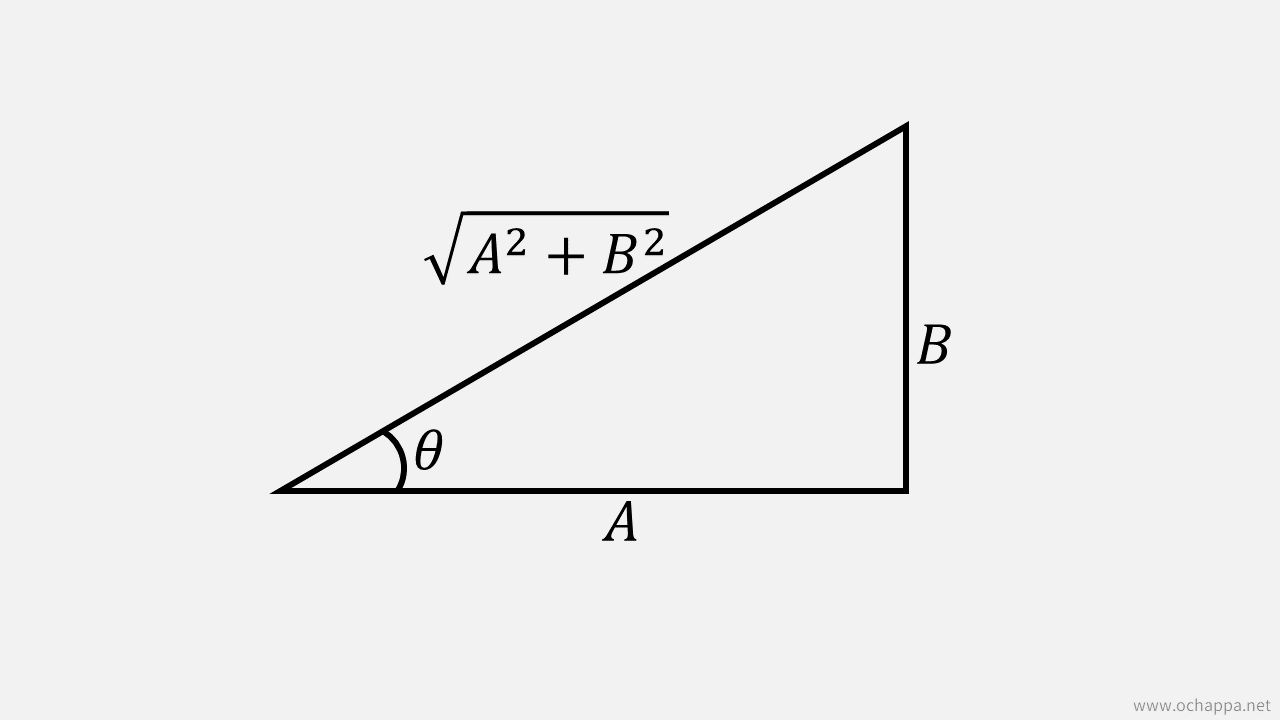
そして、最初の式を変形していきます。
(与式)=A2+B2(A2+B2Asin(ωt)+A2+B2Bcos(ωt))
この時、上記の直角三角形より以下の2つの式が成立します。
A2+B2A=cosθA2+B2B=sinθ
よって、
A2+B2(cosθsin(ωt)+sinθcos(ωt))
加法定理より、
A2+B2sin(ωt+θ)
ただし、
tanAB=θ