ブロック暗号のモードまとめ

ブロック暗号のモードとは

まず、ブロック暗号とは特定のビット数を「ひとかたまり」にして処理をする方法です。しかし、日常生活で暗号化するデータはブロック暗号のビット数に収まりません。そこで、ブロック暗号を繰り返し使って暗号化を行います。その時の繰り返し方を「モード」と言います。

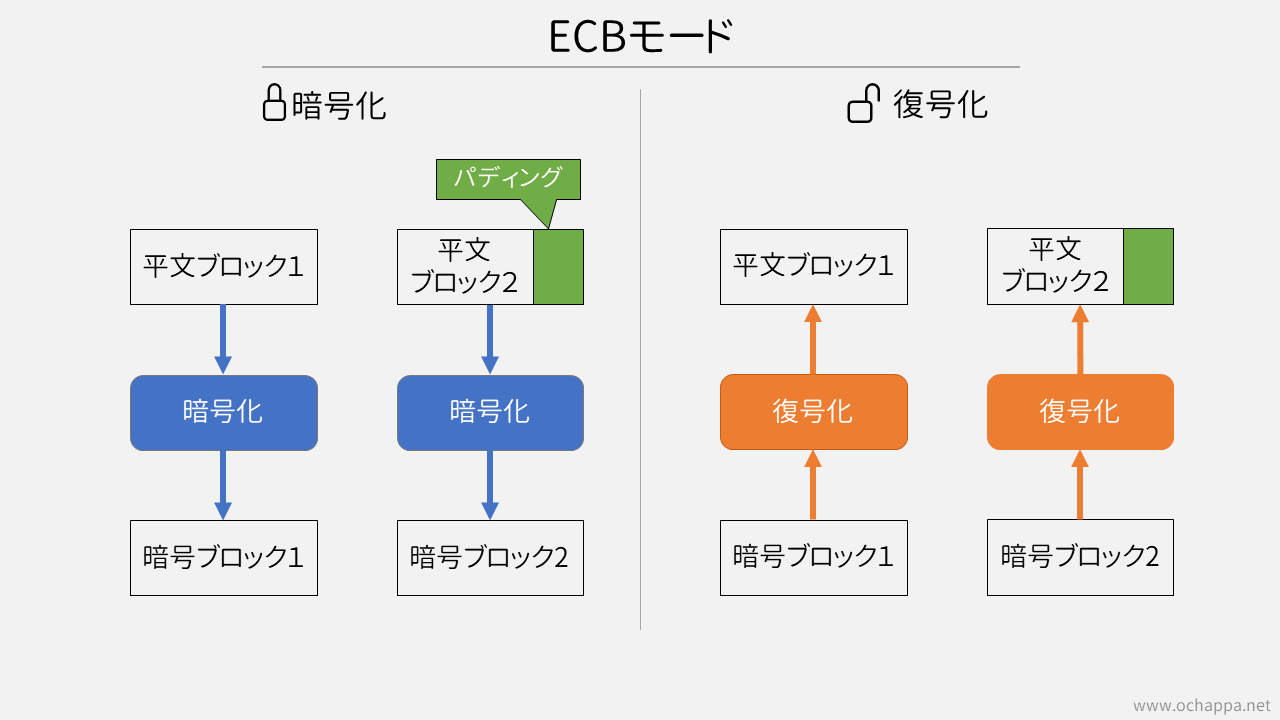
ECBモード

使うべきではないモードです!

ECB・・・Electric Codebookの略です。

平文ブロックをそのまま暗号化したものが、そのまま暗号ブロックとなります。したがって、同じ平文は同じ暗号ブロックとなり、平文 -> 暗号文という対応表ができることになります。

平文ブロックがブロック長に満たない場合は「パディング」という詰め物をします。

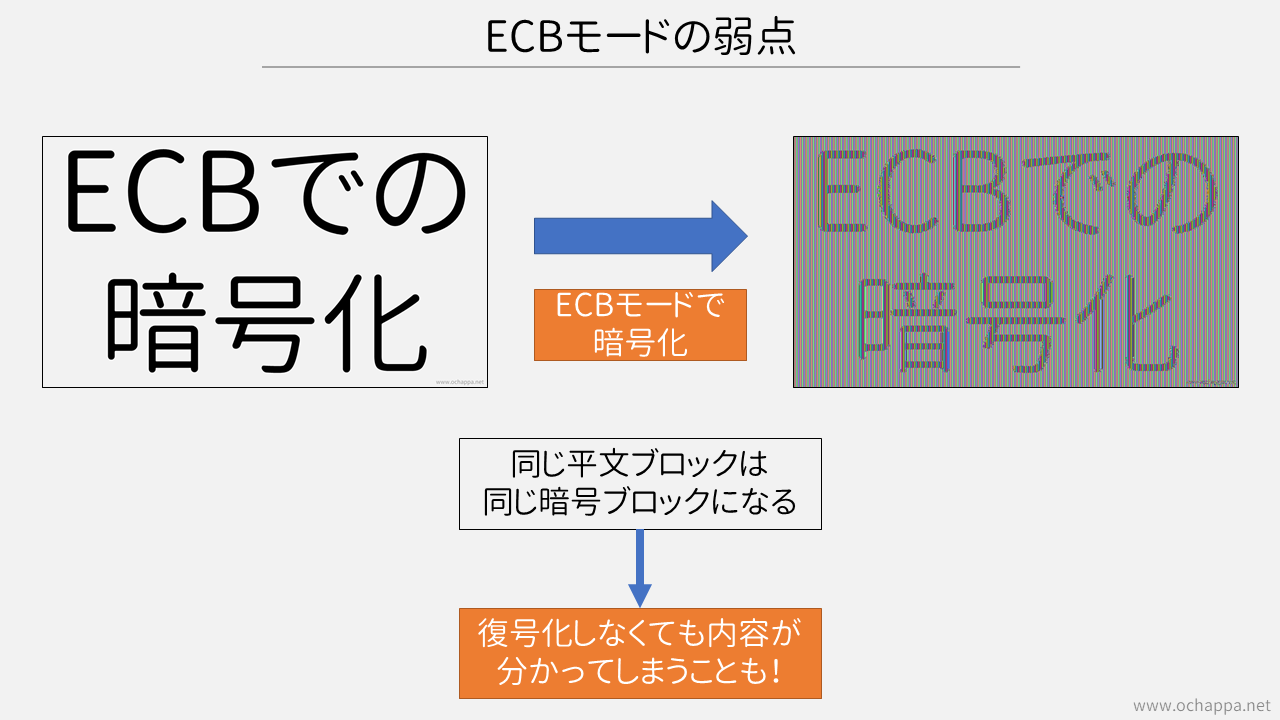
ECBモードの弱点

ECBモードでは同じ平文は同じ暗号文となります。したがって、復号化しなくても同じ平文が繰り返していることが分かります。一例として画像を暗号化した場合、復号化せずに内容が分かってしまいます。

ECBモードで画像を暗号化するコードです。

from PIL import Image
import numpy as np
from Crypto.Cipher import AES
from Crypto.Random import get_random_bytes

origin_img = np.array(Image.open(r"origin.bmp"))

key = get_random_bytes(16)
cipher = AES.new(key, AES.MODE_ECB)

enc = cipher.encrypt(origin_img.tobytes())

enc_image = np.frombuffer(enc, dtype=np.uint8).reshape(origin_img.shape)

pil_img = Image.fromarray(enc_image)
pil_img.save(r"ECB_enc.bmp")

他の弱点として、攻撃者がブロックをすり替えることが可能です。

例として、「振込先」「振込元」「金額」の3つがそれぞれブロックで暗号化されたと考えてみましょう。攻撃者は「振込先」と「振込元」を復号化することなく入れ替えることが可能です。

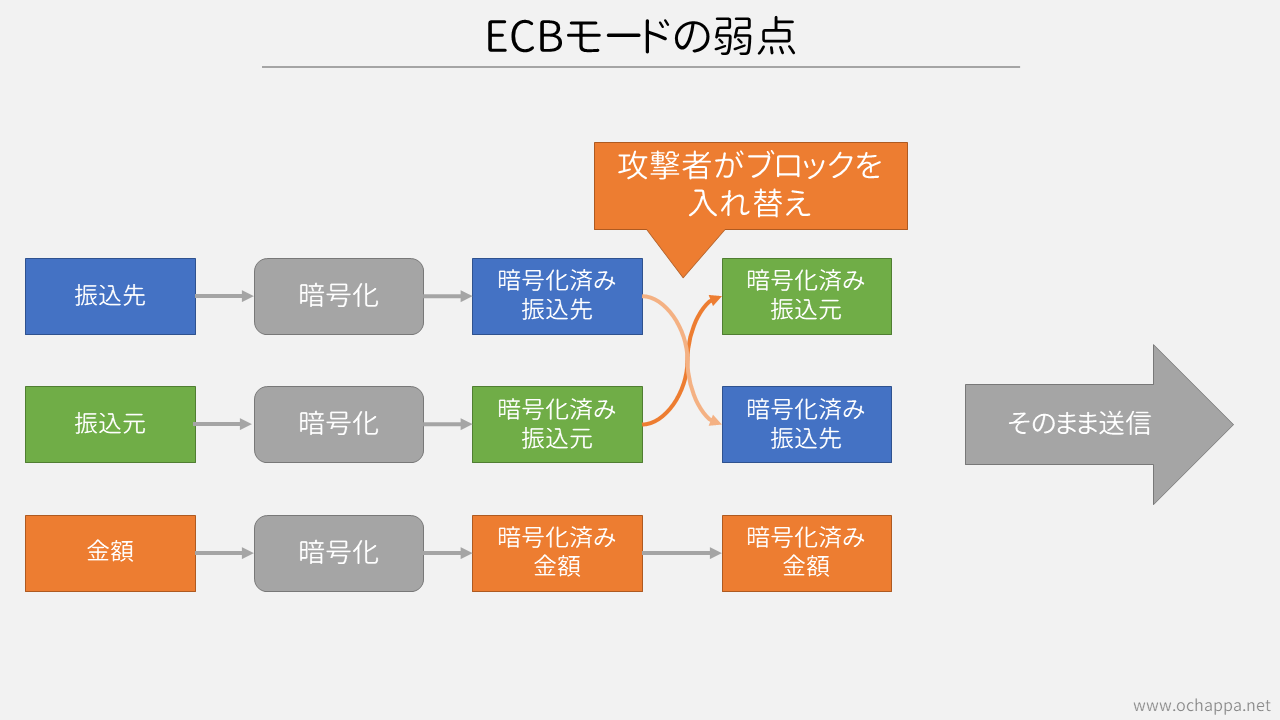
以上の点からECBモードには致命的な弱点があり、使用すべきではありません。

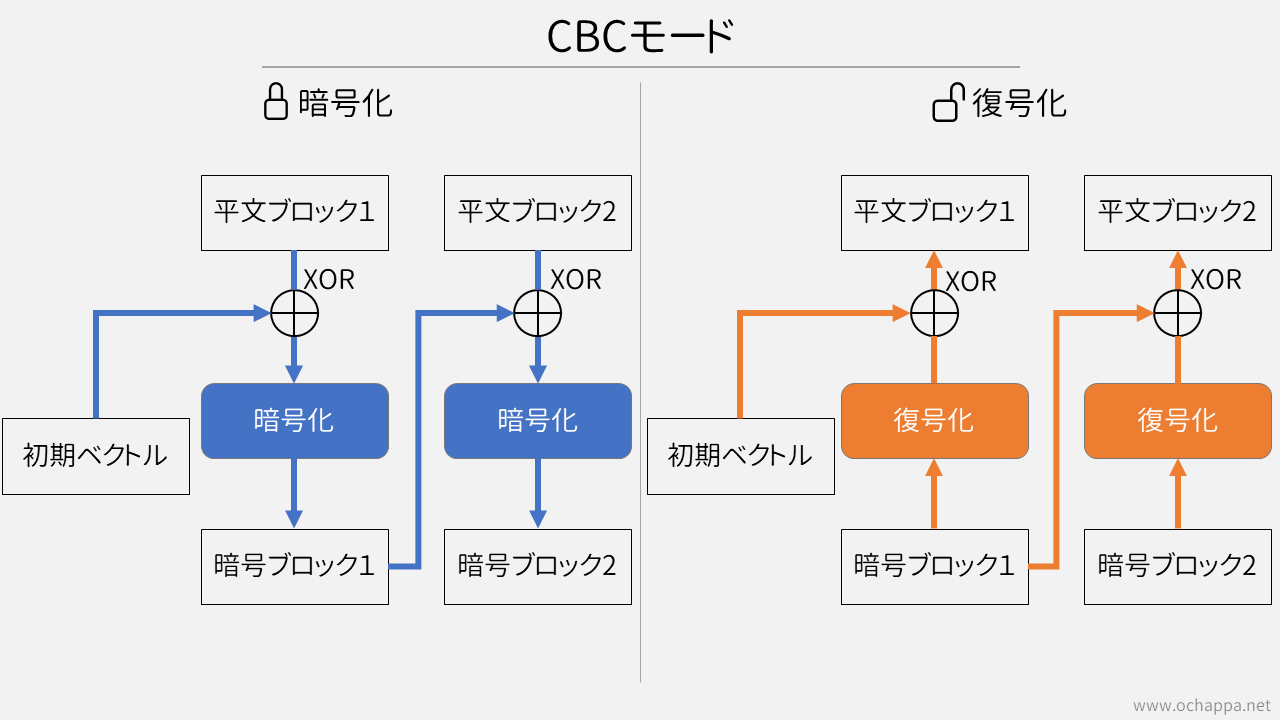
CBCモード

CBC・・・Cipher Block Chainingの略です。 ブロックをチェーンのように連鎖させて暗号化します。SSLでも利用されていました。

特徴は、1つ前の暗号ブロックと平文のXORを取ってから暗号化するところです。

1つ前の暗号ブロックをのXORを取るため、同じ平文でも違った暗号文となります。また、前後関係ができるので暗号ブロックを攻撃者が入れ替えると正しく復号化できません。したがって、ECBモードの弱点を克服しています。

最初のブロックだけは1つ前のブロックが存在しないので、「初期ベクトル」というランダムなブロックとのXORを取ります。初期ベクトルは「IV」(Initialization Vector)とも書かれます。

CBCモードの弱点として、攻撃者が初期ベクトルをいじれる場合、最初の平文ブロックの任意のビットを反転できるという攻撃があります。

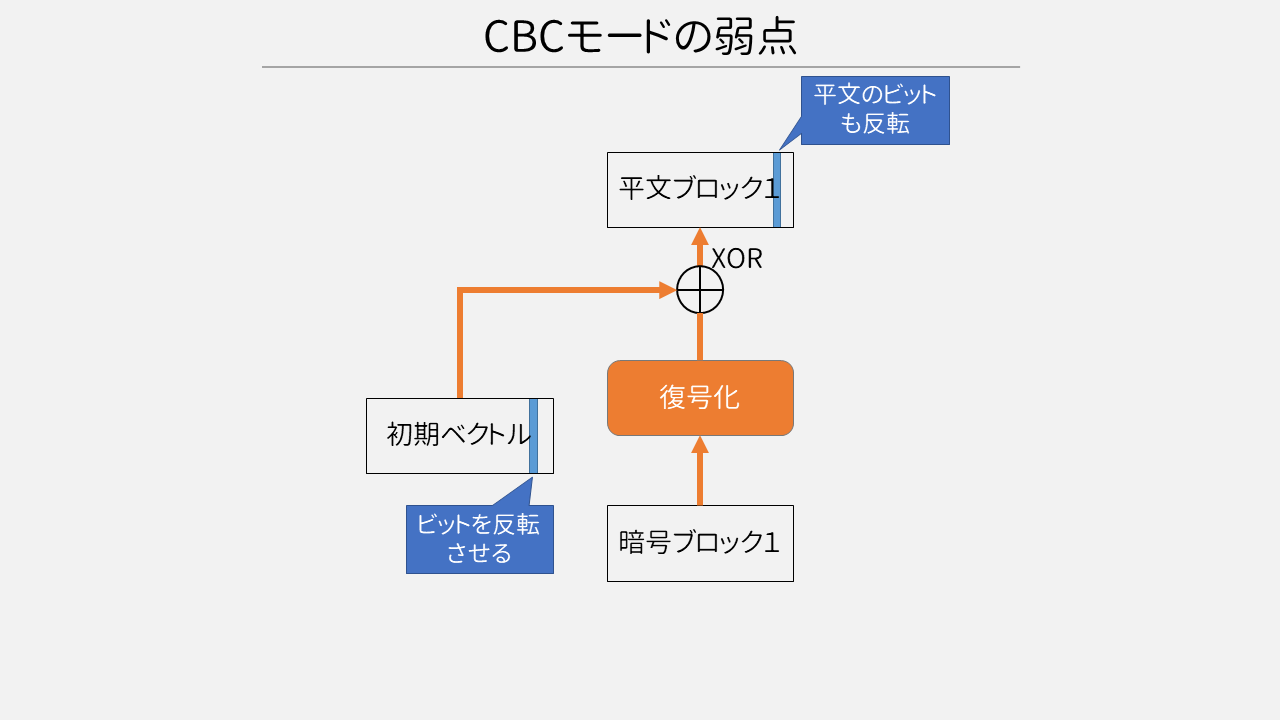
CBCモードの注意点

初期ベクトルは必ずランダムなものにしなければなりません。初期ベクトルが同じ場合、同じ平文を送信すると同じ暗号文となってしまします。

CFBモード

CFB・・・Cipher FeedBackの略です。

1つ前の暗号ブロックをさらに暗号化して平文とのXORを取ります。

平文は直接暗号化されているわけではありません。

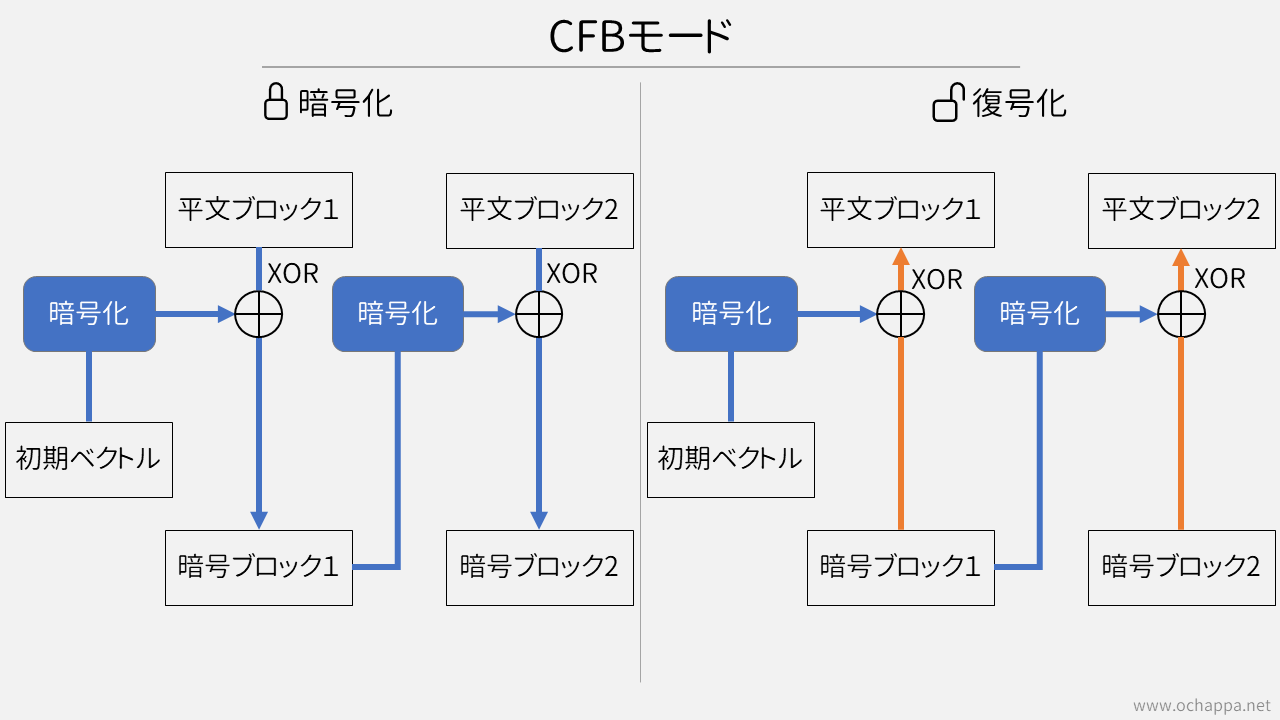
CBCモードでは「XORを取ってから暗号化」していたのに対し、CFBモードでは「暗号化してからXOR」を取る違いがあります。

OFBモード

OFB・・・Output FeedBackの略です。

初期ベクトルを暗号化し平文とのXORをとり、また暗号化しXORをとっていく方法です。

CFBは「暗号化された平文を再び暗号化する」のに対し、OFBは「暗号アルゴリズムから出力されたものを、再び暗号化」するという点です。文章では分かりにくいと思うので、図を見てください。

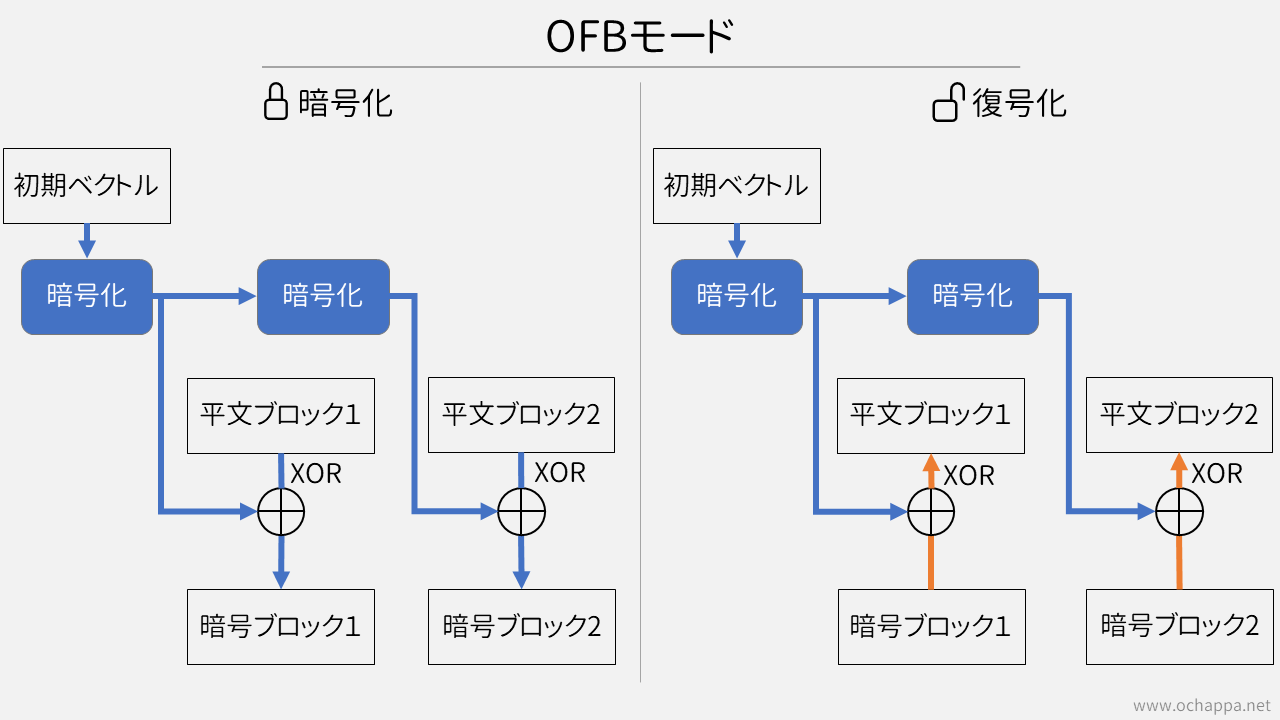
初期ベクトルが分かれば、事前にXORを取るためのビット列を事前に準備しておくことができます。

CTRモード

CTR・・・CounTR(カウンター)の略です。

「ノンス＋カウンター」で定まるビット列を暗号化し、平文とのXORを取る方法です。ノンスというのはランダムなビット列です。

ブロックの番号が分かれば、カウンターの値が定まるので任意のブロックから復号化できます。並列処理が可能なシステムであれば暗号化、復号化ともに高速で行うことができます。

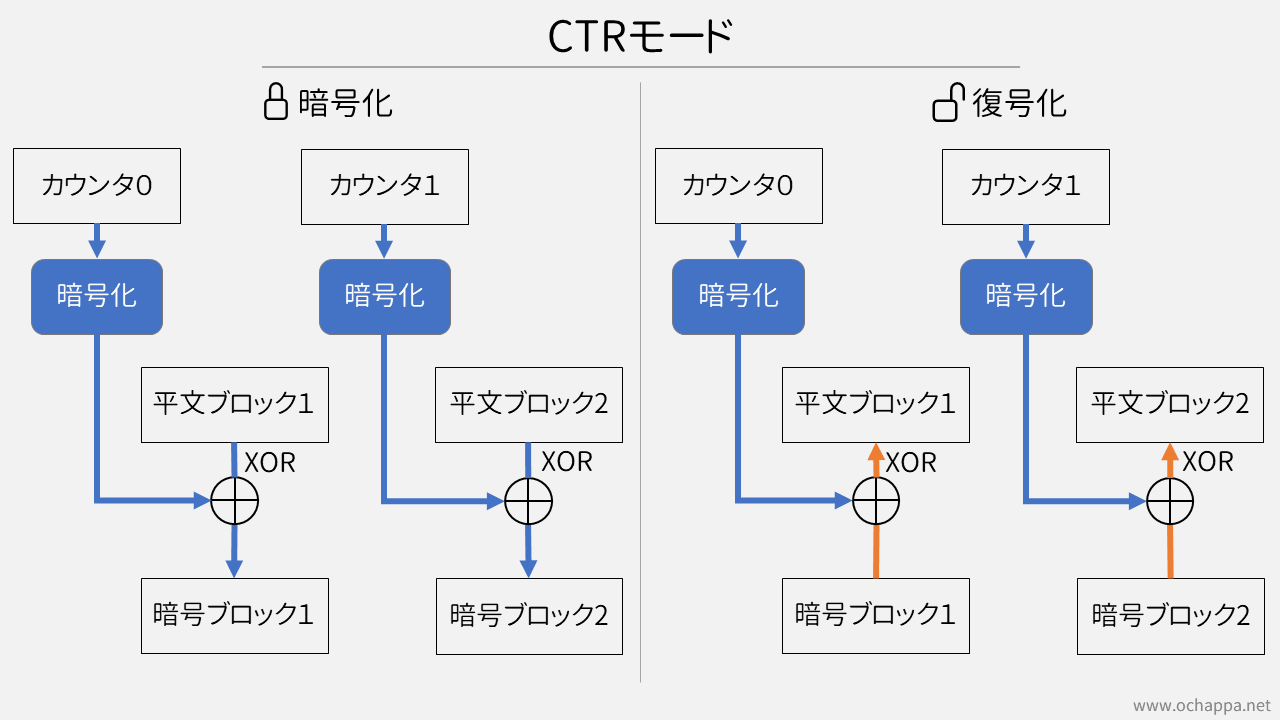
参考文献

結城浩（2015）暗号技術入門　第3版