フェルマー法による素因数分解＋Pythonでの実装

フェルマー法とは

$N$が奇数の時、整数$a,b$を用いて$N=a^2-b^2$変形できる性質を利用します。 そうすると、$N=(a+b)(a-b)$の積の形に分解でき因数は$(a+b)$と$(a-b)$であることが分かります！
$N$が偶数の場合は2で割り続ければよいです！
この手法は$\sqrt{N}$の付近から探索していくため平方数に近い数の場合に有効な手法です。

複数の素数からなる数の場合

先ほど説明した通りフェルマー法は1つの数を2つの数に分解するだけでした。そんな方法で素因数分解できるのでしょうか？

ちゃんとできます！！

$N = 17 \times 47 \times 59 \times 97$の場合は以下のように分解されて素因数分解できます。

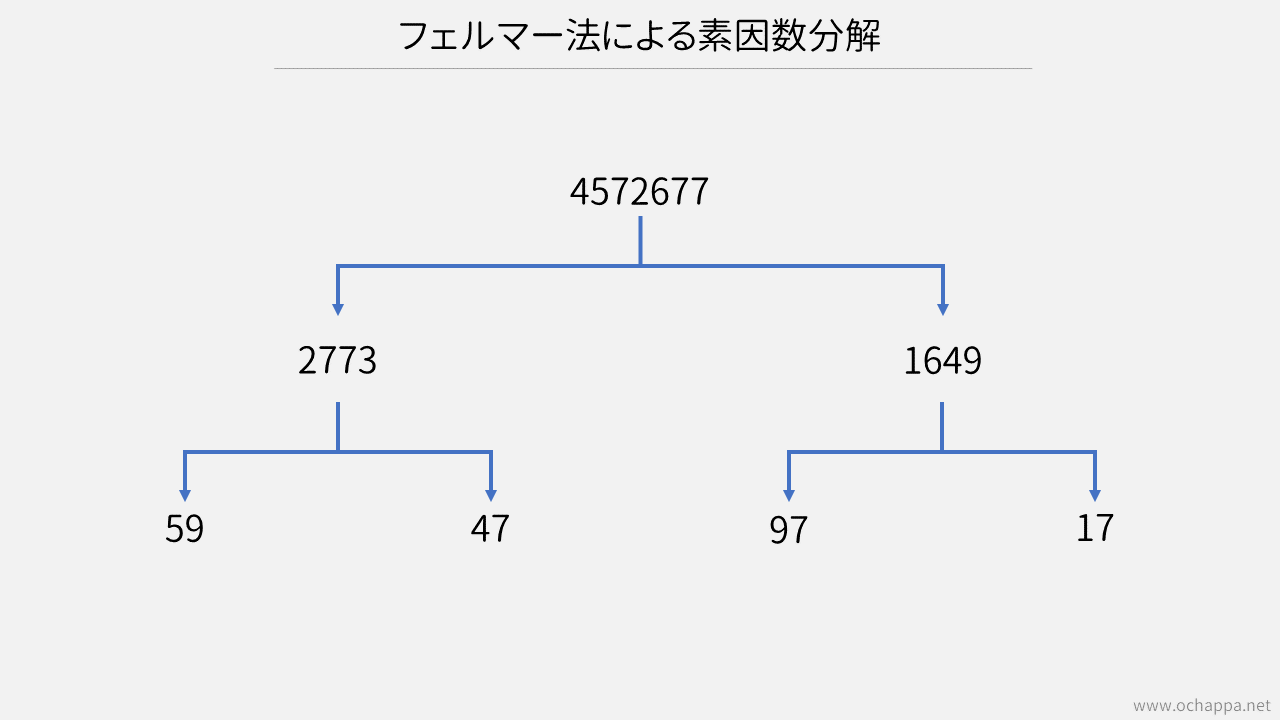
計算方法

前提条件として$N$は正の整数かつ奇数、$a, b$は0以上の整数です。
まず、$N = a^2 - b^2$を式変形します。

したがって、

となり$a$の値が求まれば$b$の値が求まる状態になりました。
ルートの中身は0以上でなければならないので、$a$の値の範囲は$a \geqq \sqrt{N}$であることも分かります。
後は$a \geqq \sqrt{N}$を満たす整数$a$を下から順番に試して$\sqrt{a^2 - N}$が整数となったところが答えです！

練習問題

161をフェルマー法を用いて素因数分解してください。

解答

1. $a^2 \geqq 161$を満たす最小の$a$を求める

$12^2 = 144,\ 13^2 = 169$より、$a = 13$と求まりました！

2. $b$が整数になるまで試す！

$a=13$の時、$b = \sqrt{169-161} = \sqrt{8}$ より、整数でない。
$a=14$の時、$b = \sqrt{196-161} = \sqrt{35}$ より、整数でない。
$a=15$の時、$b = \sqrt{225-161} = \sqrt{64} = 8$ より、整数となる！
以上より$b = 8$となりました！

3. $(a+b),(a-b)$を求める

$a = 15, b=8$ですので、
$(a+b) = 23, (a-b) = 7$となる。 したがって、$161 = 23 \times 7$ となり素因巣分解できました。

今回求めた161は13の平方数に近い値なので3回の総当たりで求めることができました。平方数から遠い場合はどうなるか気になる人は159で計算してみてください。

Pythonでの実装

それではPythonで実装します！2パターンあります。
入力のNはどちらも奇数であることが前提です。

パターン１

練習問題の解法と同じような手法で解いてくパターンです。平方数の判定にgmpy2を利用します。

from math import isqrt
import gmpy2

def fermat(N):
    a = 1 + isqrt(N - 1) # N <= a^2 を満たす最大のaを求める
    while not gmpy2.is_square(a*a - N):
        a += 1
    b = isqrt(a*a - N)
    return a+b, a-b

パターン2

$N = a^2 - b^2$となるようにa, bを増やすやり方です。gmpyを必要としません。

from math import isqrt
def fermat(N):
    a = 1 + isqrt(N - 1) # N <= a^2 を満たす最大のaを求める
    b = isqrt(a*a - N)
    while True:
        w = a*a - b*b - N
        if w == 0:
            return a+b, a-b
        elif w > 0:
            b += 1
        elif w < 0:
            a += 1

まとめ

フェルマー法による素因数分解についてまとめました！Pythonでの実装は使う場面もあると思いますのでぜひ活用してください。