蔵本モデルについて少し調べたのでまとめる

投稿日：2024/05/22 更新日:2024/05/22

蔵本モデル

蔵本モデルとは

蔵本モデルとは同期現象を記述するために提案された数理モデルです。

以下の式で示されます。

\frac{d \phi_i}{d t} = \omega_i + \frac{K}{N}\sum_{j=1}^N \sin(\phi_j - \phi_i)

ここで、 $N$ が発振素子の個数、 $\phi_i$ は発振素子の位相、 $\omega_i$ は発振素子の角振動数です。

式を追ってみる

まず、多数の振動子があるとします。各振動子はそれぞれ固有の角振動数 $\omega_i$ を持っています。

今の状況だと各振動子は以下の式で記述できます。

\frac{d \phi_i}{d t} = \omega_i

ここに振動子同士の相互作用を考えます。相互作用は弱く、振幅には影響を与えないと考えます。つまり、振幅は時間変化せず一定です。よって、相互作用により変化するのは位相のみとなります。

ここに相互作用の影響を加えたのが蔵本モデルです。相互作用の大きさ、すなわち結合を位相の差の関数で記述します。結合を $\sin(\phi_j - \phi_i)$ とします。

振動子 $i$ が $j$ よりも少し遅れている、すなわち $(\phi_j - \phi_i) > 0$ の時、関数は正の値となり位相を進めようととします。反対に、振動子 $i$ が $j$ よりも前に進んでいる、すなわち $(\phi_j - \phi_i) < 0$ の時、関数は負の値となり位相を戻そうとします。

$\sin$ 関数は奇関数であるため、 $\sin(-x) = -\sin(x)$ が成り立ちます。これは、位相差の正負が逆転すると、相互作用の効果も逆転することを意味します。

そして、振動子は多数あるのでそれらの相互作用の和を取ったものとなります。これらを踏まえると前の式は以下のようになります。

\frac{d \phi_i}{d t} = \omega_i + \frac{K}{N}\sum_{j=1}^N\sin(\phi_j - \phi_i)

ここで、 $K$ 結合強度と呼ばれ結合の強さを示します。 $K$ が大きいほど位相を揃わせようとします。

秩序変数

秩序変数 $r$ があります。これは蔵本モデルにおいて各振動子がどれほど同期しているかを示す式です。

r = \frac{1}{N} \left| \sum_{j=1}^Ne^{i\phi_j(t)} \right|

ここの $i$ は虚数単位です。秩序変数は０から１の値を取り１に近いほど同期していることになります。

絶対値を付けない場合は単位円上を回転している振動子の重心座標となります。

蔵本予想

予想と言っていますが、既に証明されています。（蔵本定理と言った方が良い？）

秩序変数 $r$ と結合強度 $K$ にはある関係があります。

$K$ がある閾値 $K_c$ 以下では $r$ は0に漸近安定であり、それを超えるとある値を $r$ が大きくなりはじめる。

このような関係があります。

シミュレーションしてみる

実際に蔵本モデルをシミュレーションしてみました。結果は以下のような状態です。初めの一瞬はバラバラでしたが、すぐに揃っていることが分かります。

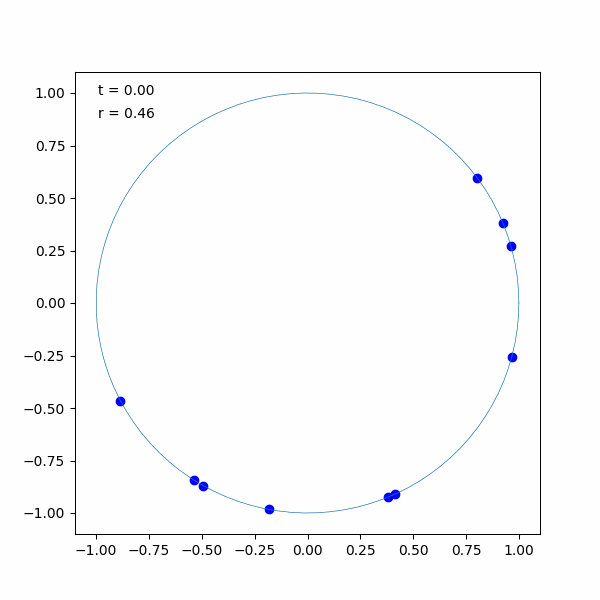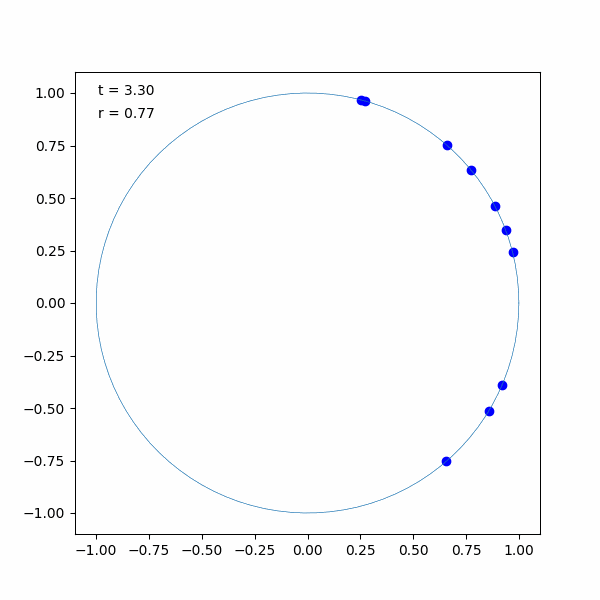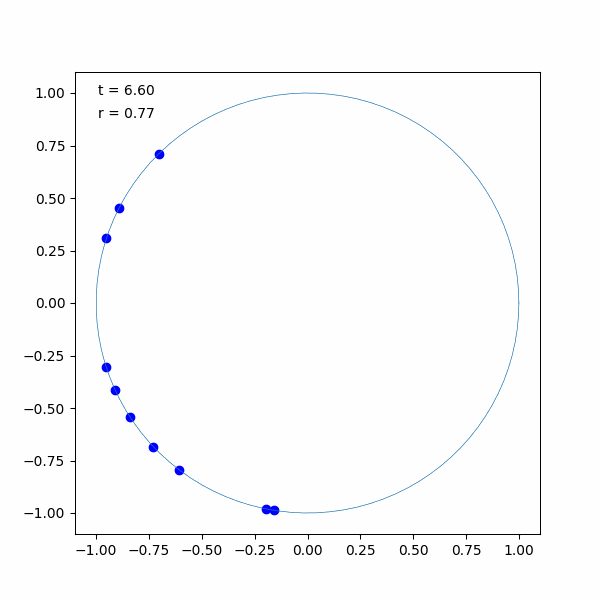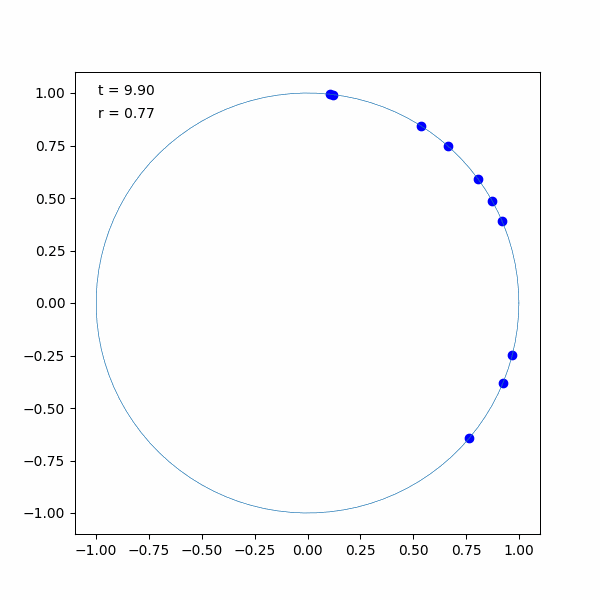
蔵本モデルのアニメーション

ソースコードは以下の通りです。

import numpy as np
from scipy.integrate import solve_ivp
from numpy.typing import NDArray
import matplotlib.pyplot as plt
import matplotlib.animation as animation

n = 10 # 振動子の数
omega = np.random.normal(loc=1, scale=1, size=n) # 固有角周波数
k = 2.1 # 結合強度

def kuramoto_model(t: float, phi: NDArray[np.float64]) -> NDArray[np.float64]:
    dphi = np.zeros(n)
    for i in range(n):
        dphi[i] = omega[i] + np.sum(phi - phi[i]) * k/n
    return dphi

phi0 = np.random.random(n) * 2 * np.pi # 初期位相
dt = 0.1 # 刻み幅
t = np.arange(0, 10, dt)

sol = solve_ivp(kuramoto_model, [0, 10], phi0, t_eval=t) # 計算実行


# 描画処理
fig = plt.figure(figsize=(6, 6))
ims = []

# 円の描画
theta = np.linspace(0, 2*np.pi, 100)
plt.plot(np.cos(theta), np.sin(theta), linewidth=0.5)
plt.xlim(-1.1, 1.1)
plt.ylim(-1.1, 1.1)

for i, t in enumerate(sol.t):
    # 位相を直交座標に直す
    x = np.cos(sol.y[:, i])
    y = np.sin(sol.y[:, i])
    im = plt.scatter(x, y, marker='o', color="blue")

    # 時刻の表示
    time_text = plt.text(0.05, 0.95, f't = {t:.2f}', transform=plt.gca().transAxes)

    # 秩序変数の計算
    r = np.abs(np.sum(np.exp(1j * sol.y[:, i]))) / n
    r_text = plt.text(0.05, 0.90, f'r = {r:.2f}', transform=plt.gca().transAxes)

    ims.append([im, time_text, r_text])

# アニメーション作成
ani = animation.ArtistAnimation(fig, ims, interval=100)
ani.save('kuramoto.gif', writer='pillow')

参考文献

蔵本予想とは何か? 〜予想紹介編〜 https://mattyuu.hatenadiary.com/entry/2017/01/08/211848

逸人千葉一般化スペクトル理論による蔵本予想へのアプローチ https://doi.org/10.11429/sugaku.0692181